 Матрицата
Матрицата
Това е статия представяща част от математическия апарат на
Общата теория на относителността.
Налага се да разгледаме по-отблизо някои правила.
Разчитам на това, че вече са известни началните сведения, например от
сайта на Станчо Павлов за
матрични
и
векторни
операции.
Векторите в ортогонална и остроъгълна координатна система
/"остроъгълна" е същото, каквото е "клиногонална" или "неправоъгълна"/
Условно "остроъгълна" тук ще наричаме координатна система, съставена от три базисни линейно независими (некомпланарни) вектора.
Ако те са взаимно перпендикулярни, координатната система е ортогонална. В противен случай между
координатните прави има поне един остър ъгъл.
Векторът в тримерна координатна система е наредена тройка числа
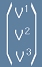 - компоненти. Да означим трите базисни вектора като
- компоненти. Да означим трите базисни вектора като
 (шапка над буква означава базисен вектор);
тогава векторът V се записва така:
(шапка над буква означава базисен вектор);
тогава векторът V се записва така:
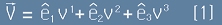 .
.
Компонентите
v1 v2 v3 представят този вектор в нашата координатна система, но за същият вектор в друга координатна
система, те ще са различни.
Ако възприемем примови означения за другата координатна система, горното равенство ще изглежда като :
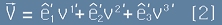 .
.
Равенствата [1] и [2] са валидни за правоъгълна и за остроъгълна координатна система.
Тук е използувано правилото, че всеки вектор може да се представи по един-единствен начин като линейна комбинация
от два или повече на брой линейно независими вектори.
Можем да гледаме на [1] и [2] като матрично умножение "ред по стълб". Например [1] се записва по следния начин:
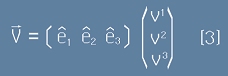 .
.
Ето защо индексите на вектора V са записани в горе вдясно - за да напомнят, че са подредени в колона.
Скаларно умножение на вектори
В ортогонална координатна система скаларното произведение на два вектора би било
ab = axbx + ayby + azbz.
Но това няма да е вярно в остроъгълна координатна система, тъй като в този случай "проекцията" на единичен вектор върху ос вече не
е равна на косинус от сключения ъгъл.
По-долу ще опитаме да изразим скаларното произведение на два вектора U и V в остроъгълна координатна система.
Да запишем вектор U подобно на V от [1]:  .
.
Чисто алгебрично, скаларното произведение на два вектора U и V може да се изрази със следното равенство:
 .
.
Ако разкрием скобите, в ортонормирана координатна система можем да запишем това кратко:
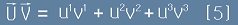 ,
,
тъй като скаларните произведения са нула при разноименни и единица при едноименни базисни вектори.
Сега да опитаме да представим дясната страна от равенството [5] като матрично произведение. Правилото "ред по стълб" ни подсказва,
че векторът U трябва да е матрица с хоризонтално разположени компоненти, а векторът V - с вертикално разположени.
Произведението UV от [5] ще бъде:
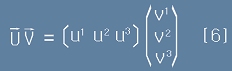 .
.
Да не забравяме, че че [5] и [6] са верни единствено в ортоногонална координатна система.
Но и в остроъгълна координатна систама има начин да намерим израз близък до [6] - начинът е да приведем двата вектора U и V
към ортонормирана система. За да направим това, първо трябва да приведем остроъгълните базисни вектори
 към ортонормиран базис
към ортонормиран базис  .
.
Използувайки представянето [1], можем да запишем:
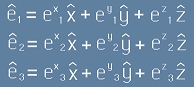 , после
, после
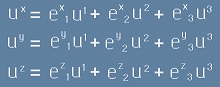 , и в матричен вид
, и в матричен вид 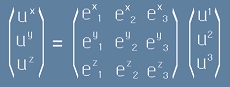 .
.
Да си спомним правилото за транспонирано произведение на матрици:  ;
;
Вместо [6] можем да запишем - вече в остроъгълна координатна система:
 .
.
По-горе избрахме числата в средните две матрици от дясната страна на [7] така, че да представляват векторни
компоненти в ортонормирана координатна система.
Следователно за тях важи равенството:
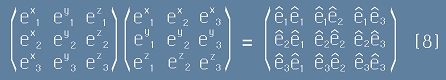 .
.
Метрика
Деветте числа, написани в матричен вид от дясната страна на [8] се наричат метрика (метричен тензор) и се означават :
 .
.
Чрез метриката равенството [7] изглежда по-кратко:
 .
.
Последното равенство [9] изразява скаларно произведение между два вектора и е вярно при ортогонална,
и при остроъгълна координатна система.
То илюстрира правилото на Айнщаин за сумиране по повтарящи се индекси. По-точно
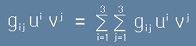 .
.
Метричният тензор винаги е симетричен, а при ортонормирана координатна система съвпада с единичната матрица.
В общия случай нито едно от деветте му числа не е нула.
Взаимен базис, контравариантни и ковариантни вектори
Да се върнем към задачата за скаларно произведение на два вектора от по-горе.
Сложната формула [7] може да бъде избягната и да ползуваме подобие на [5] - тоест по-кратко,
ако двата вектора U и V се представят в различни координатни базиси.
На всеки неортогонален базис  , се съпоставя друг - взаимен базис
, се съпоставя друг - взаимен базис
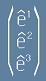 , чийто базисни вектори спазват условието
, чийто базисни вектори спазват условието 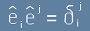 .
.
 Символът
Символът  се нарича Делта на Кронекер. Той е равен на 1,
когато двата индекса са равни и нула в противен случай, тоест съвпада с единична матрица.
Взаимния базис понякога се нарича дуален базис. Думата "взаимен" идва от руски език, а "дуален" - от английски.
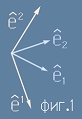
На фиг.1 са нарисувани два базиса - основен и взаимен - в 2 измерения.
се нарича Делта на Кронекер. Той е равен на 1,
когато двата индекса са равни и нула в противен случай, тоест съвпада с единична матрица.
Взаимния базис понякога се нарича дуален базис. Думата "взаимен" идва от руски език, а "дуален" - от английски.
На фиг.1 са нарисувани два базиса - основен и взаимен - в 2 измерения.
Скаларното произведение на едноименните вектори от основния и взаимния базис е единица.
Скаларното произведение на разноименните вектори от основния и взаимния базис е нула.
Това означава, че разноименните вектори от основния и взаимния базис са перпендикулярни един на друг.
Координатите на вектор във взаимен базис се разполагат в хоризонтален ред, а индексите им се записват в долна позиция;
Така записани вектори се наричат още ковариантни, за разлика от досега записваните, наричани контравариантни -
във вертикален ред и с горен индекс.
За ортогонален базис взаимният съвпада с основния, при което ковариантни и контравариантни компоненти са равни.
Взаимния на взаимния базис съвпада с основния, но базисните вектори на взаимния и основния базис са с различна дължина
и посока. Това означава, че ако основният базис е нормиран-съставен от вектори с единична дължина, то взаимният не е и обратно.
По-горе в [3] е записан контравариантен вектор V в основния базис.
Ето как би изглеждал същия този вектор като ковариантен във взаимния базис:
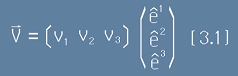
Съпоставка:
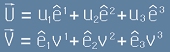
U е в ковариантни компоненти и дуален базис;
V е в контравариантни компоненти и основен базис.
Ако U е ковариантен а V - контравариантен вектор, нека допуснем (засега без доказателство), че тяхното скаларно произведение е:
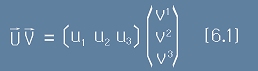 .
.
Записът [6.1] е формално близък до [6], но важи за остроъгълни базиси. По-нататък ще приемем правило, че за остроъгълни
координатни системи скаларно произведение между два вектора е определено
единствено при ситуацията [6.1], тоест единият вектор трябва да е ковариантен, а другият - контравариантен.
Това значи например, че в остроъгълни базиси е "забранен" запис от вида [5], който и без това беше предназначен
само за ортогонален случай.
По този начин избягваме дисхармонията в записите [6] и [7], където поради липса на дуален базис
бяхме принудени да записваме контравариантни компоненти в хоризонтален ред.
Да напишем [6.1] като
 .
.
Да съпоставим [9.1] с [9] - виждаме две неща:
Първо - виждаме начин, по който - чрез метриката - от контравариантни компоненти се получават ковариантни:
 .
.
Второ - виждаме, че вярността на [9.1], и съответно [6.1] следва от [9].
В последните равенства отново е използувано правилото на Айнщайн за сума по повтарящи се индекси. Още нещо:
повтарящите се индекси винаги са двойки ковариантен и контравариантен. Ако от двете страни на едно равенство има
свободни индекси (по които няма сума), те трябва да са равни по име и вид.
Вижте още веднъж как се дефинира дуален базис.
коментари
Радостин Желязков 13.09.2010
________________________________________________________________________________________
учебни статии по физика
 Матрицата
Матрицата
 - компоненти. Да означим трите базисни вектора като
- компоненти. Да означим трите базисни вектора като
 (шапка над буква означава базисен вектор);
тогава векторът V се записва така:
(шапка над буква означава базисен вектор);
тогава векторът V се записва така: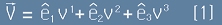 .
.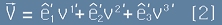 .
.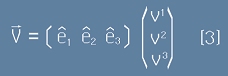 .
. .
. .
.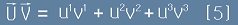 ,
,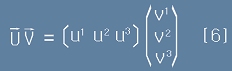 .
. към ортонормиран базис
към ортонормиран базис  .
.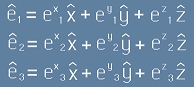 , после
, после
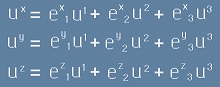 , и в матричен вид
, и в матричен вид 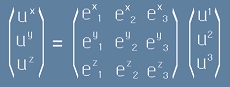 .
. ;
; .
.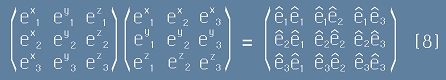 .
. .
. .
.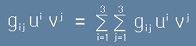 .
. , се съпоставя друг - взаимен базис
, се съпоставя друг - взаимен базис
 , чийто базисни вектори спазват условието
, чийто базисни вектори спазват условието 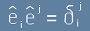 .
. Символът
Символът  се нарича Делта на Кронекер. Той е равен на 1,
когато двата индекса са равни и нула в противен случай, тоест съвпада с единична матрица.
Взаимния базис понякога се нарича дуален базис. Думата "взаимен" идва от руски език, а "дуален" - от английски.
На фиг.1 са нарисувани два базиса - основен и взаимен - в 2 измерения.
се нарича Делта на Кронекер. Той е равен на 1,
когато двата индекса са равни и нула в противен случай, тоест съвпада с единична матрица.
Взаимния базис понякога се нарича дуален базис. Думата "взаимен" идва от руски език, а "дуален" - от английски.
На фиг.1 са нарисувани два базиса - основен и взаимен - в 2 измерения.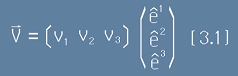
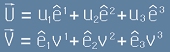
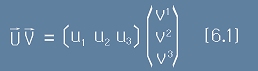 .
. .
. .
.