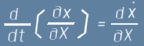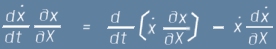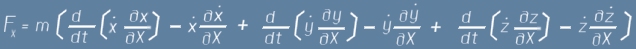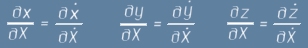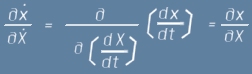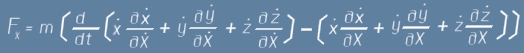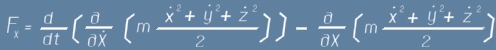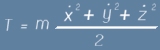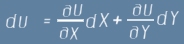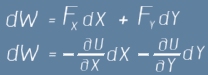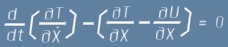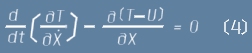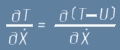Функция на Лагранж /лагранжиан/
Функция на Лагранж /лагранжиан/
Този материал изисква малко знания за
функции с две променливи
и
частни производни.
Те могат да бъдат намерени в
учебника по висша математика на Станчо Павлов - търсете
- II част - Дефиниции / Частни производни.
 Обобщени координати
Обобщени координати
Това са линейни координати, обикновено различни от декартовите, но декартовите координати са техни еднозначни функции.
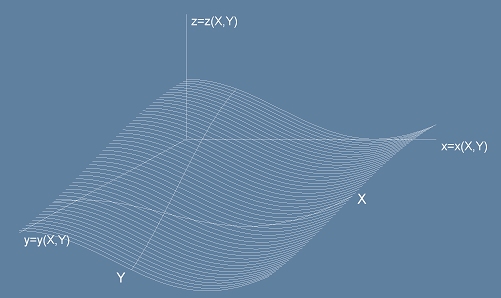
Например ако топче се търкаля по твърд улей, една обобщена координата - дължина, измерена по
улея, е достатъчна за да опише позицията му. Точките върху коя да е повърхност могат да бъдат описани с две обобщени координати. По-долу ще разглеждаме случай, в който тяло с маса m е свободно да се движи именно по две обобщени координати. Да означим с малки букви x y z декартовите, а с големи букви X Y обобщените координати. Както вече споменахме x y z са функции на X и Y
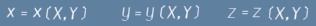
Обобщени сили
Нека една сила (означена по-долу с малка буква f ) действува върху движещо се тяло. При преместване тя извършва работа

където dx dy dz са промените на позицията, изразени в декартови координати. От гледна точка
на обобщените координати същата работа може да се изрази като

- тук големите букви F означават две съставки - по обобщените координати - на сила,
която можем да определим като обобщена сила.
Извод
Всяка декартова координата е функция на X Y, следователно трите изменения dx dy dz от дясната страна на равенството (1) могат да се представят чрез измененията dX dY на обобщените координати X и Y
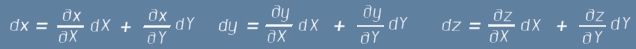
след което изразът за работата (1) ще придобие вид
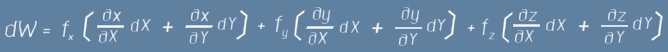
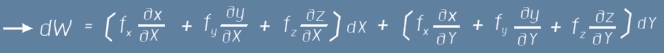
Ако съпоставим последното равенство почленно с (2), виждаме от десните страни, че
двете съставки на обобщената сила трябва да бъдат
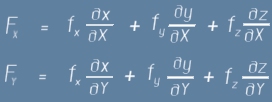
В следващите разсъждения, известно време ще разчитаме на успоредно развитие за двете горни равенства и ще разглеждаме само първото от тях.
Съгласно Втория закон на Нютон, декартовите съставки на f могат да се представят като
произведения на масата по трите компонента на ускорението ax ay az (по-долу точка върху буква означава производна по времето)
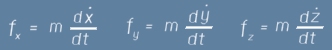
След горните три равенства X - съставката на F може да бъде записана като
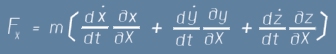
[отклонение 1]
Първото събираемо на израза вътре в скобите от по-горе се среща и като първо събираемо в едно друго равенство, изразяващо производна по времето t на едно друго произведение:
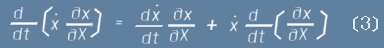
[отклонение 2]
Да се съсредоточим върху последния множител от горното равенство (3). Той изразява последователно диференциране на x-функцията по X и t, но тъй като X и x са еднозначни функции от
времето t, реда на диференциране може да се промени и да доведе до равностоен израз. За по-лесно разбиране, нека си спомним, че производната на x е всъщност скорост. Разгледана като частна производна по X, тя остава проекция на същата тази скорост и това не може да зависи от поредността на пресмятане:
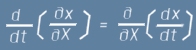 , или за по-кратко
, или за по-кратко 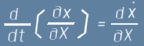
[/край на отклонение 2]
И така въпросното първо събираемо може да бъде изразено по разликов начин:
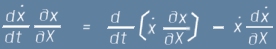
[/край на отклонение 1]
след което изразът за X-съставката на F придобива вид:
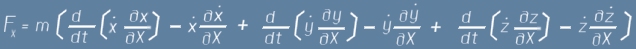
[отклонение 3]
Еднозначните зависимости x(t) и X(t) водят лесно до следните три равенства:
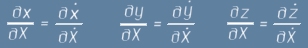
- ето илюстрация за първото от тях:
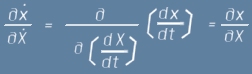
[/край на отклонение 3]
Малко прегрупиране след отклонение 3, в израза за FX води до:
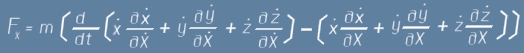
Сега да забележим, че събираемите във вътрешните скоби представляват производни:

След всичко това, се вижда че
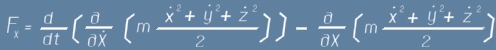
Ако приемем означението T за изразите във вътрешните скоби
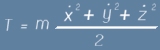
то двете съставки на обобщената сила F ще изглеждат така /уравнения на Ойлер-Лагранж/:

Ако механичната енергия се запазва, работата (2) извършена от силата F се равнява изцяло
на промяната /намалението/ в потенциалната енергия. Да приемем, че потенциала на системата зависи само от позицията (не от скоростите) на телата. По-долу ще използваме буква U за потенциалната енергия и dU за нейната промяна в интервала dt. Ако една величина има определена числова стойност за всяка точка в пространство, това е скаларно поле. Значи подлежи на диференциране по всяко направление, в частност по обобщените координати X Y. За разглеждания интервал dt, потенциалното изменение ще бъде
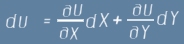
при което извършената работа dW може да се изрази по следните два начина:
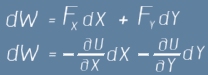
Но X и Y са независими една от друга и следователно горните две равенства са възможни само при условие, че

Заместването в уравненията на Ойлер-Лагранж води до
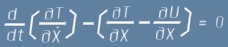
или още 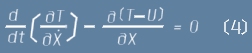
Както казахме по-горе, Потенциалът U не зависи от скоростите и следователно
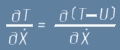
В такъв случай ако приемем означението L=T-U, равенството (4) както и аналогичното за Y, могат да бъдат записани така:

L се нарича функция на Лагранж.
Радостин Желязков 12.06.2008
________________________________________________________________________________________
учебни статии по физика
 Функция на Лагранж /лагранжиан/
Функция на Лагранж /лагранжиан/
 Обобщени координати
Обобщени координати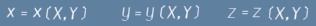


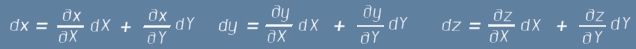
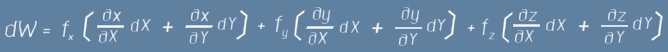
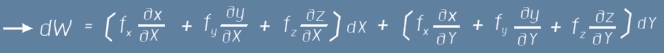
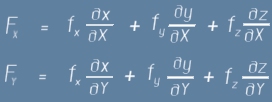
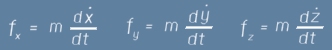
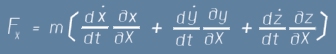
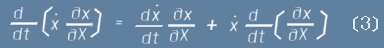
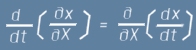 , или за по-кратко
, или за по-кратко