 Стълба на Габриел
Стълба на Габриел
Помощна статия.
Геометрична прогресия
Това е поредица (сума) която започва с ненулево число b, а всеки следващ елемент се получава от умножение на предния по едно и също число q.
По-долу сумите са означени с целочислен индекс m, равен на най-голямата степен на q.
Нека b и q са реални числа. Да разгледаме два съседни по m сбора:
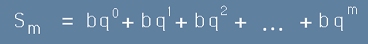 , [1]
, [1]
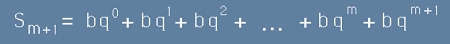 . [2]
. [2]
Ако умножим равенството [1] по q и прибавим към него b, ще получим [2] :
 [3] .
[3] .
От друга страна, [1] и [2] се различават само по последния член от [2], тоест
 . [4]
. [4]
Да извадим [3] от [4]. Получаваме уравнението
 . [5]
. [5]
Решението на това уравнение спрямо сбора Sm е
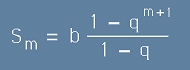 . [6]
. [6]
И то изразява сбора на първите m събираеми в геометричната прогресия. При големи индекси m и при 0<q<1, втория член на числителя клони към нула.
По долу ще приемем, че b=1 и 0<q<1.
Тогава формулата за сбора, при индекс, растящ от нула до m е
 . [7]
. [7]
При безкрайно нарастване на индекса m, границата на сбора от [7] е
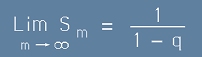 . [8]
. [8]
Стълба на Габриел
Да разгледаме сбора
 [9] ,
[9] ,
наричан някъде Стълба на Габриел.
Макар с безкраен брой събираеми, този сбор има крайна стойност. Станчо Павлов ми показа един хубав начин да го намерим - изложен тук:
Да разделим двете страни от [9] с множителя q. Получаваме
 [10] .
[10] .
Интегралите на двете страни от [10] по q ще бъдат
 ,
,
където C е някаква константа.
Ние не знаем колко е тя, но знаем, че има друга, C1 , която е с едно по-малка, тоест C = C1+1.
В такъв случай последното равенство може да се запише като
 [11] ,
[11] ,
(виж по-горе [7] и [8]). Обратно, производните на двете страни от [11] по q са
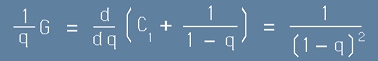 [12] .
[12] .
От тук се вижда, че сбора на Габриел е
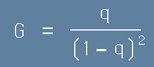 [13] .
[13] .
коментари
Радостин Желязков 21.05.2011
________________________________________________________________________________________
учебни статии по физика
 Стълба на Габриел
Стълба на Габриел
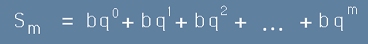 , [1]
, [1]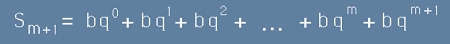 . [2]
. [2] [3] .
[3] . . [4]
. [4] . [5]
. [5] . [6]
. [6] . [7]
. [7]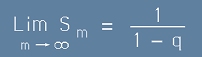 . [8]
. [8] [9] ,
[9] , [10] .
[10] . ,
, [11] ,
[11] ,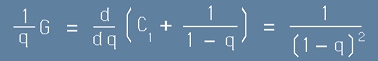 [12] .
[12] .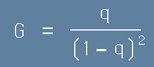 [13] .
[13] .