Текстурни координати.
Програмите понякога чертаят на екрана повърхности, деформирани от 3D перспектива или
специални ефекти. Съвременните средства за програмиране предоставят цялостен mesh
или поне текстурен механизъм, който спасява програмиста от грижата да пренесе образа
от първоначалната рисунка към екрана. Но има и случаи, когато това се налага.
В тази статия е описана еднa версия за текстурно пробразуване.
Примерната програма е писана за Делфи, но е лесно преводима и към друг език.
Общата постановка на задачата е координатен преход
от криволинейна в правоъгълна координатна система.
Онова което се вижда от пръв поглед е, че можем да разделим целия крив участък на малки четириъгълни области,
за които се смята, че се са проекции на квадрати от правоъгълната система.
Преобразуването от правоъгълни към криволинейни координати ще смятаме за вече решено,
тъй като при работа с изкривено пространство знаем как се строят кривите на полето,
иначе не бихме могли да построим контурния образ.
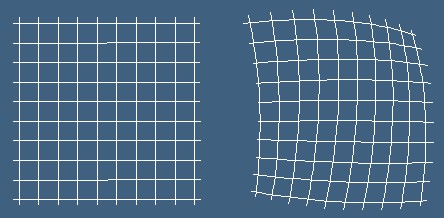
С такова преобразуване можем да получим образи на отделни точки контури, форми и цветове,
но не и плътна рисунка. За да се получи плътно изображение е нужно обратно пробразуване - от криви към прави координати.
Обаче обратната задача -
При даден произволен четириъгълник да намерим за всяка точка от вътрешността му
правоъгълни координати обикновено е по-сложна.
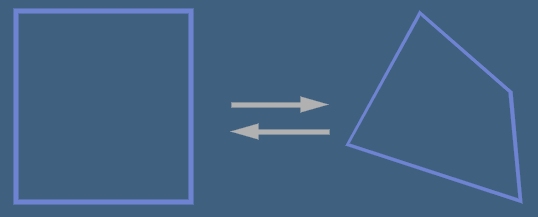
На пръв поглед това би трябвало да е линейно преобразувание, но всъщност не е.
Макар, че фигурите са от прави линии, преобразуването е от втора степен.
Преди всичко да направим малко уговорка свързана с представянето на
правите линии. Програмистите знаят, че права линия се чертае най лесно
с параметричен ход на двете координати x/y:
x=x1+ax*t
y=y1+ay*t
където ax и ay са коефициенти на наклона по x/y.
Те се определят като
ax=dx/dt
ay=dy/dt
t е линеен параметър описващ достатъчно подробно двете координати.
Ако няма други изисквания, той варира
от 0 до dt-1
dt=max(abs(dx),abs(dy))
което е достатъчно за една отсечка. По-долу ще наричаме dt параметрична дължина.
Правата линия може да бъде обхваната от клас съдържащ комплект числа за удобство:
.....
TLineClass=class
x1,y1,x2,y2, //координати на началната и крайна точка
dx,dy, //размери на обвивката
t, //оперативен параметър
dt //параметрична дължина на отсечката
:integer;
ax,ay:real; //коефициенти на наклона по x и по y
procedure InitTLine(p1,p2:TPoint);
procedure RecalcLinePar(newdt:integer);
end;
......
implementation
......
(****************************************************)
procedure TLineClass.RecalcLinePar(newdt:integer);
begin
dt:=newdt;
if dt>0 then begin ax:=dx/dt;ay:=dy/dt;end
else begin ax:=0;ay:=0;end;
end;
(****************************************************)
procedure TLineClass.InitTLine(p1,p2:TPoint);
begin
x1:=p1.x;y1:=p1.y;x2:=p2.x;y2:=p2.y;
dx:=x2-x1;dy:=y2-y1;t:=0;
RecalcLinePar(max(abs(dx),abs(dy)));
end;
......
В нашият случай обаче ще трябва да изравним четирите
параметрични дължини за страните на четириъгълника
dt1=dt2=dt3=dt4 = dtmax
и освен това (но само за този пример) да ги изравним с pdx/pdy - размерите на картинка на текстурата.
dtmax = max(pdx,pdy)
Така всяка страна на четириъгълника се превръща в "сгъстена" версия
на съответната страна от текстурния квадрат - тази представа ще ни помага в разбирането
и решението на задачата.
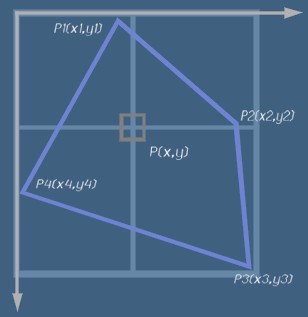
Нека x и y са координатите на произволна точка P вътре в четириъгълника.
Да разгледаме вътрешността като двупараметрично множество.
Ако намерим двата съответни параметъра tx и ty за точката P,
това ще бъде решение на задачата, тъй като в квадрата tx и ty са координатите
на търсения пиксел.
Да приемем че четириъгълника е съставен от четири отсечки с индекси
1,2,3,4 съответни на (p1 p2), (p2 p3), (p4 p3), (p1 p4).
Да проектираме P върху отсечките 1 и 4, които представляват версии на осите
x/y от текстурния квадрат. Да не забравяме, че макар с различен наклон, всичките четири страни
имат еднаква параметрична дължина = dtmax.
Да означим с M(xm,ym) проекцията на P върху "хоризонталната" ос.
След като всяка точка върху права се представя по параметричния начин описан по-горе,
можем да напишем двете равенства (виж долната рисунка)
xm = x1 + a1x*tx [1]
x = xm + ax*ty [2]
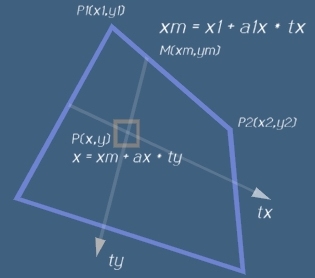
където единственият проблем е величината ax.
Тази величина (ax) представлява x-наклона на правата ty. Лявата и дясната отсечка с индекси 4 и 2 (p1p4 и p2p3) имат наклони
a4x и a2x. Наклона ax е някъде помежду им. Този наклон се променя линейно
от a4x до a2x и е пропорционален на tx, значи може да се приеме, че
ax = a4x + dax*tx [3]
където a4x е наклона на отсечка 4 (p1 p4), а dax е коефициента на нарстване = (a2x-a4x)/dt0.
След заместваме на ax от [3] и xm от [1] в равенството [2],
за x остава
x = x1 + a1x*tx + (a4x + dax*tx)*ty
или
x = x1 + a1x*tx + a4x*ty + dax*tx*ty [4]
Ако повторим същите разсъждения за y - координатата,
ay = a1y + day * ty
y = y1 + a4y*ty + (a1y + day*ty)*tx
y = y1 + a4y*ty + a1y*tx + day*tx*ty [5]
ще получим близък израз за y и така стигаме до системата уравнения [4]+[5]:
| x = x1 + a1x*tx + a4x*ty + dax*tx*ty
| y = y1 + a4y*ty + a1y*tx + day*tx*ty
Тази система (неизвестните са tx,ty)
може да бъде записана по удобен начин така:
| a1*tx*ty + a2*tx + a3*ty + a4 = 0
| b1*tx*ty + b2*tx + b3*ty + b4 = 0
където сме положили
a1 = dax b1 = day
a2 = a1x b2 = a1y
a3 = a4x b3 = a4y
a4 = x1-x b4 = y1-y
След заместване на tx от първото уравнение
и след малко преобразувания на второто получаваме:

Последното уравнение съдържа задачата в сравнително чист вид - осем известни величини a1,a2,a3,a4,b1,b2,b3,b4.
Не могат да бъдат по-малко, защото четири точки се определят от осем координатни числа.
В действителност даже точките са пет - четири за четириъгълника и още една P(x,y) за която търсим образ.
Обаче първата точка от четириъгълника се асоциира с началото на координатната система tx=0,ty=0
и така броят на независимите точки остава четири.
Уравнението се решава по познат начин с формулите на Виет.
Кода на процедурата която прави транслацията е даден по-долу.
Използуван е класа TLineClass (виж по-горе)
за отсечка, чиито екземпляри са lc1, lc2, lc3, lc4 - съответни на отсечките с индекси.
procedure ConvertXYtoSquareCoordinates(x,y:integer;var tx,ty:integer);
var a1,a2,a3,a4,b1,b2,b3,b4,a,b,c,d,d2,x1,x2,zn:real;
begin
a1:=dax; // тук са осемте променливи идващи от правите
a2:=lc1.ax; // x - наклон на първата отсечка
a3:=lc4.ax; // x - наклон на четвъртата отсечка
a4:=lc1.x1-x; // относителна x - координата спрямо обвивката
b1:=day; // симетрично за y - уравнението
b2:=lc1.ay;
b3:=lc4.ay;
b4:=lc1.y1-y;
a:=b3*a1-a3*b1; // a b c са коефициентите на квадратния тричлен
b:=a2*b3-a3*b2+a1*b4-a4*b1;
c:=a2*b4-a4*b2;
x1:=-1;x2:=-1;
if a<>0 then
begin
d:=b*b-4*a*c; // d е дискриминантата на Виет
if d>=0 then
begin
d2:=Sqrt(d);
x2:=(-b+d2)/(2*a);
end;
end
else
begin
if b<>0 then x2:=-c/b;
end;
if x2>=0 then
begin
zn:=(x2*a1+a2);
if zn<>0 then
x1:=(-a4-x2*a3)/zn // възстановяваме заменената незвестна
else
x2:=-1;
end;
tx:=round(x1);
ty:=round(x2);
end;
В горната процедура се предполага, че четирите отсечки
са инициализирани и приравнени към размерите на картинката.
Всъщност кода за инициализацията е изложен тук (при точки p1 p2 p3 p4)
....
{global scope}
var lp1,lp2,lp3,lp4:TLineClass;dax,day:real;
....
(****************************************************)
procedure InitLines(p1,p2,p3,p4:TPoint);
begin
lc1:=TLineClass.Create;lc2:=TLineClass.Create;lc3:=TLineClass.Create;lc4:=TLineClass.Create;
lc1.InitTLine(p1,p2); //сетваме четирите отсечки
lc2.InitTLine(p2,p3);
lc3.InitTLine(p4,p3);
lc4.InitTLine(p1,p4);
dt0:=0;
dt0:=max(dt0,lc1.dt); //намираме най-дългата дистанция
dt0:=max(dt0,lc3.dt);
dt0:=max(dt0,lc2.dt);
dt0:=max(dt0,lc4.dt);
dt0:=max(dt0,pdx); //вземаме предвид и текстурните размери
dt0:=max(dt0,pdy);
lc1.RecalcLinePar(dt0); //изравняваме отсечките по параметрична дължина
lc2.RecalcLinePar(dt0);
lc3.RecalcLinePar(dt0);
lc4.RecalcLinePar(dt0);
dax:=(lc2.dx-lc4.dx)/dt0; //коефициент на нарстване на наклона по x
day:=(lc3.dy-lc1.dy)/dt0; //коефициент на нарстване на наклона по y
end;
(Променливите pdx и pdy са размерите на картинката)
Тази процедура показа следния образ:

Който може да работи с Делфи, или преведе сорса на познат за него език ще съумее да го приложи и да види
сам резултата.
*Забележки:
1. Така описаната методика не обхваща всички възможни четириъгълници. Случаите, в които
четириъгълника е неизпъкнал или кръстосан, могат да създадат особености, които не са
изследвани тук. Вероятно двата корена на квадратното уравнение (ако съществуват и са положителни)
описват случая, при който четириъгълника е сгънат на две (например по диагонала).
Тогава една точка в образа съответства на две точки от текстурата-източник.
2. Изравняването с размерите на картинката има пропорционален характер.
То е удачно когато очакваме източника и приемника на образа
да имат приблизително еднакви размери. Ако картинката-източник е много по-голяма от приемника,
това би довело до излишно забавяне на кода. В този случай е по-добре да се използува пропорция
за достъп до пикселите на текстурата, вместо да сгъстяваме цикъла който сканира четириъгълника.
РЖ 03.07.2005
начална страница
други статии






