 Оператор на импулса
Оператор на импулса
Това е част от квантовата механика. Операторът на измпулса вече е бил споменаван в тази поредица,
но тук той е изведен по-подробно.
Желателно е запознаване с преднишни статии:
Функция на Лагранж,
Принцип на Хамилтон,
Уравнения на Хамилтон,
Оператори,
Уводът на Ландау,
Матриците на Хайзенберг.
Пространството е еднородно
Да си представим затворена система от материални точки.
Ако позицията на тази система е отместена някъде на друго място (паралелен пренос),
енергията, тоест Хамилтоновата функция не се променя. Засега ще ни трябва малко отместване. Ако с малко гръцко алфа означим индекс на една частица, всеки един от радиус-векторите на частиците ще получи нарастване, означено с по-долу с малка гръцка буква делта:
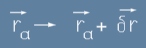 . [1]
. [1]
Вълновата функция на такава система се представя като:
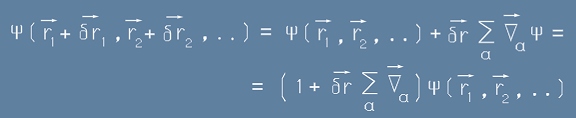 . [2]
. [2]
Сбора вдясно става по индекса алфа на частиците. Индекс алфа при набла-оператора означава, че това е диференциране по направление на радиус-вектора с индекс алфа. Умножението на малкото векторно нарастване делта и векторня сбор, получен при набла-операциите е скаларно.
Изразът:
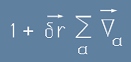 [3]
[3]
представлява оператор на безкрайно малък пренос.
Когато казваме, че някой оператор не променя Хамилтониана, това значи, че прилагането му преди и след Хамилтоновия оператор дава еднакви резултати, тоест:
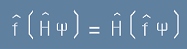 [4], или по друг начин записано
[4], или по друг начин записано
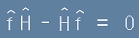 . [5]
. [5]
В нашия случай
 , [6]
, [6]
и по-точно
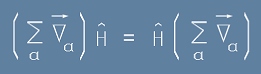 . [7]
. [7]
Когато операторът на една величина комутира с Хамилтониана, тази величина е запазваща се (виж [15] от
предната статия
). Запазващата се величина, свързана с еднородността на пространството е импулс.
И така, равенство [7] изразява закона за запазване на импулса.
Излиза, че набла операторът набла има смисъл на оператор на импулса.
Класическа препратка
За да преценим дали това е правдоподобно, нека си спомним за
Принципа на Хамилтон.
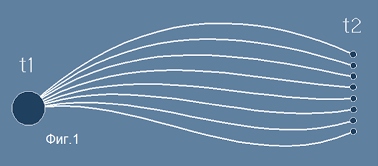
Да разгледаме фазов преход за една механична система от момент t1 до момент t2.
Ще смятаме обаче, че състоянието в момент t2 варира,
тоест обобщените координати и импулси не са фиксирани в крайния момент t2 - виж фиг.1.
Вариацията на действието S остава както междинно пресметнатата от
Принцип на Хамилтон:
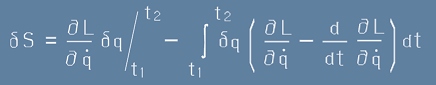 . [8]
. [8]
Но умаляемото не е нула - крайните координати и импулси варират, както се уговорихме.
Този път интегралът в дясно ще е нулев, защото
при реално поведение на системата е изпълнено
уравнението на Ойлер-Лагранж
и изразът в скобите е нула.
Можем условно да приемем, че в момент t1 обобщените координати имат нулева стойност, а в момент t2 са просто  .
.
Освен това, да заместим производната на L от първия член вдясно на [8] с обобщения импулс:
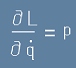 [9]
[9]
- за справка виж дефиницията, записана като равенство [3] от статията
Уравнения на Хамилтон.
Така от [8] получаваме
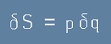 . [10]
. [10]
Поуката е, че
Градиентът от действието е импулс
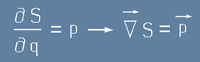 . [11]
. [11]
Тоест записът в по-горното уравнение [7] съответства на класическия импулс.
Сега нека се върнем към Вълновата функция, както е записана в равенство [4] от
предната статия (без амплитудния множител a):
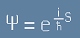 . [12]
. [12]
От по-горе [7] видяхме, че операторът на импулса трябва да е пропорционален - с точност до множител за размерност - на набла. За да уточним този множител, да сметнем набла, според [12].
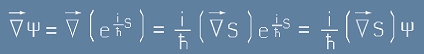 . [13]
. [13]
Както видяхме с [11], класическият смисъл на градиент от действието е импулс.
Равенство [13] показва, че за да получим импулс в дясно, трябва да умножим по h/i.
Да не забравяме, че когато търсим вид на оператор, имаме предвид правилото [24] от статията
Уводът на Ландау.
В такъв случай
Операторът на импулса
трябва да има вид:
 . [14]
. [14]
Това е векторен оператор. От неговата x-компонента можем да построим уравнение за собствената
стойност на px-оператора:
 . [15]
. [15]
Или като по-удобно за решаване:
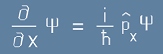 . [16]
. [16]
Последното равенство [16] се интегрира пряко и получаваме следния вид за собствената Пси-функция за x-компонентата на импулса:
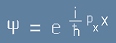 . [17]
. [17]
Трите компонента на импулса - по x y z са независими и едновременно измерими.
Според принципа за суперпозицията,
едновременна стойност на няколко различни величини съответствува на произведение на техните вълнови функции.
Следователно собствената Пси-функция за оператора на импулса като вектор е:
 , [18]
, [18]
където в степенния показател е скаларно произведение на импулса по радиус-вектора.
Радостин Желязков 11.10.2015
________________________________________________________________________________________
коментари
учебни статии по физика
 Оператор на импулса
Оператор на импулса
 . [1]
. [1]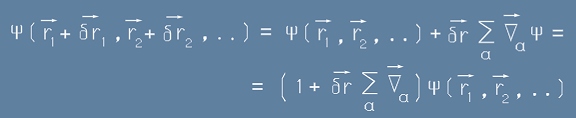 . [2]
. [2] [3]
[3]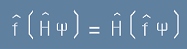 [4], или по друг начин записано
[4], или по друг начин записано
 . [5]
. [5] , [6]
, [6] . [7]
. [7]
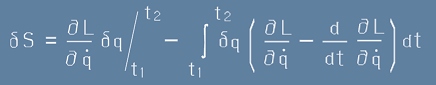 . [8]
. [8] .
.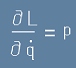 [9]
[9]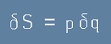 . [10]
. [10] . [11]
. [11]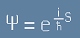 . [12]
. [12]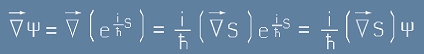 . [13]
. [13] . [14]
. [14] . [15]
. [15]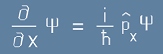 . [16]
. [16]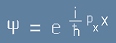 . [17]
. [17] , [18]
, [18]