 Ковариантна производна на вектор
Ковариантна производна на вектор
Този текст подпомага разбирането на математическия апарат в
Общата Теория на Относителността (ОТО).
Трябва да сте гледали Матрицата I, Матрицата II
и Матрицата III..
Вижте какво пише в
страницата на Станчо Павлов за частните производни.
Правило на Лайбниц
Тук ще търсим как се променя образа на производната на един вектор V по координатните оси,
в условията на криволинейни (обобщени) координати.
Тъй като векторът се представя като произведение (компоненти х базисни вектори):
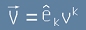 ,
,
по правилото на Лайбниц диференциалната промяна е  [1].
[1].
От друга страна, това трябва да съвпада с 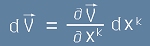 [2].
[2].
Да сложим знак за равенство между десните страни на [1] и [2]. Тогава
 , но ако в ляво трябва остане частната производна на V
по координатите, тя би трябвало да се запише по следния начин:
, но ако в ляво трябва остане частната производна на V
по координатите, тя би трябвало да се запише по следния начин:
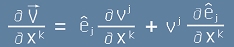 [3].
[3].
Изразеното в [3] е всъщност
Определение
за ковариантна производна на вектора V по координатните оси. Да погледем лявата страна на [3].
Векторът в числителя, заедно с индекса k на координатната ос ни казва, че това е нещо
с по-висока размерност от самия вектор V. Не би трябвало да се изненадваме, след като вече знаем,
че производната на скаларно поле по координатите е вектор, тоест пак с една размерност повече.
Да разгледаме състава на [3], тоест дясната страна.
Първото събираемо е естествен сбор "компонент по координатен вектор", а що се отнася до второто,
да съобразим, че компонентите на кой да е вектор U се получават като умножим вектора по взаимния базис:
 и така стигаме до извода, че
компонентите за второто събираемо от [3] са
и така стигаме до извода, че
компонентите за второто събираемо от [3] са 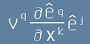 - това позволява
да запишем за j-компонента на ковариантната производна следния израз:
- това позволява
да запишем за j-компонента на ковариантната производна следния израз:
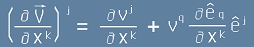 [4].
[4].
Да означим 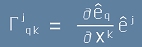 . Тази структура се нарича
символ на Кристофел.
. Тази структура се нарича
символ на Кристофел.
След всичко дотук, можем да запишем компонентите на ковариантната производна - вече известни от [4], но с друга символика, както изглежда да е общоприето:
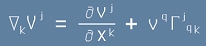 [5].
[5].
Прилагателното "ковариантна" е ползувано, защото написното в [5] е тензор, съдържащ ковариантен индекс - тип (1,1).
Това ще бъде показано по-долу.
Но засега е по-важно друго.
Ще потърсим по каква формула се преобразуват наречените по-горе
Символи на Кристофел.
Да си спомним как се преобразуват базисните и дуално-базисни вектори:
 .
В такъв случай, за символите на Кристофел преобразуванието е
.
В такъв случай, за символите на Кристофел преобразуванието е
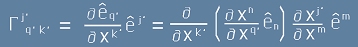 . Да приложим правилото на Лайбниц в скобите и ще получим:
. Да приложим правилото на Лайбниц в скобите и ще получим:
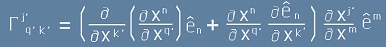 . [6].
. [6].
Да разкрием скобите в [6] и да разгледаме двете събираеми - първото събираемо е:
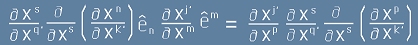 , [7]
, [7]
а второто: 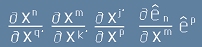 [8].
[8].
Да заместим [7] и [8] в [6]:
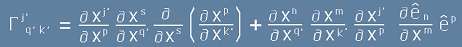 [6.1].
[6.1].
Да означим с буква "a" преходните елементи. Ще получим
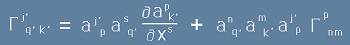 [9].
[9].
Откъдето се вижда, че това не е тензор. Обаче сега можем да докажем, че
Ковариантната производна е тензор
Да видим как се преобразува ковариантната производна от [5]. Записваме я с примове:
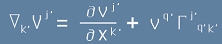 [10].
[10].
Нека разгледаме първото събираемо вдясно на [10], като имаме предвид, че
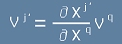 [11].
[11].
Първият член на [10] е
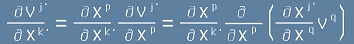 [12].
[12].
Извършваме действието в скобите:
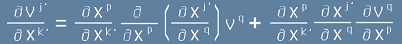 [13].
[13].
Сега да обърнем внимание на второто събираемо в [10], имайки предвид [6.1] и [11].
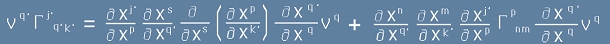 [14].
[14].
Второто събираемо от [14] и второто събираемо от [13] очевидно се преобразуват по тензорен начин.
Остава да разгледаме първите събираеми в [13] и [14]. Ако покажем, че те взаимно се унищожават,
нашата цел би била постигната.
Първо да забележим, че елементите на преобразуване имат следното свойство:
 . Следователно производната на този израз е нула. Тя има вид:
. Следователно производната на този израз е нула. Тя има вид:
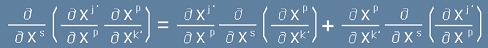 , откъдето се вижда, че
, откъдето се вижда, че
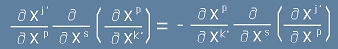 . Ако заместим това в [14],
. Ако заместим това в [14],
първото събираемо в [14] остава 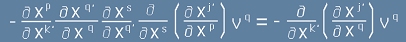 [16].
[16].
Но първото събираемо в [13] е:
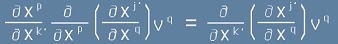 [17]. Йее те се унищожават!
[17]. Йее те се унищожават!
Следователно [10] може да се запише като
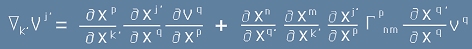 [18].
[18].
С "a" - коефициенти това изглежда като
 [19],
[19],
което е тензорна трансформация. Това показва, че ковариантната производна е тензор.
коментари
Радостин Желязков 12.10.2010
________________________________________________________________________________________
учебни статии по физика
 Ковариантна производна на вектор
Ковариантна производна на вектор
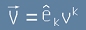 ,
, [1].
[1].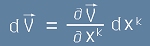 [2].
[2]. , но ако в ляво трябва остане частната производна на V
по координатите, тя би трябвало да се запише по следния начин:
, но ако в ляво трябва остане частната производна на V
по координатите, тя би трябвало да се запише по следния начин: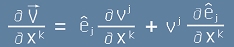 [3].
[3]. и така стигаме до извода, че
компонентите за второто събираемо от [3] са
и така стигаме до извода, че
компонентите за второто събираемо от [3] са 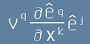 - това позволява
да запишем за j-компонента на ковариантната производна следния израз:
- това позволява
да запишем за j-компонента на ковариантната производна следния израз: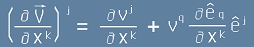 [4].
[4].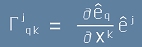 . Тази структура се нарича
символ на Кристофел.
. Тази структура се нарича
символ на Кристофел.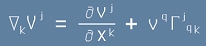 [5].
[5]. .
В такъв случай, за символите на Кристофел преобразуванието е
.
В такъв случай, за символите на Кристофел преобразуванието е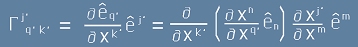 . Да приложим правилото на Лайбниц в скобите и ще получим:
. Да приложим правилото на Лайбниц в скобите и ще получим: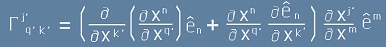 . [6].
. [6].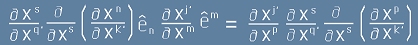 , [7]
, [7]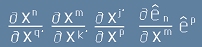 [8].
[8].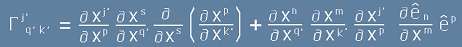 [6.1].
[6.1].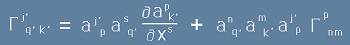 [9].
[9].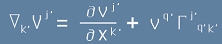 [10].
[10].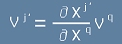 [11].
[11].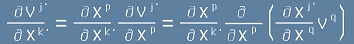 [12].
[12].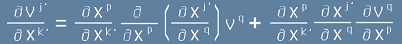 [13].
[13].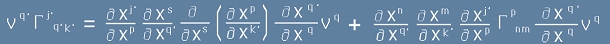 [14].
[14]. . Следователно производната на този израз е нула. Тя има вид:
. Следователно производната на този израз е нула. Тя има вид: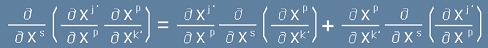 , откъдето се вижда, че
, откъдето се вижда, че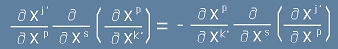 . Ако заместим това в [14],
. Ако заместим това в [14],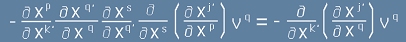 [16].
[16].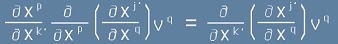 [17]. Йее те се унищожават!
[17]. Йее те се унищожават!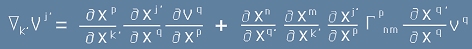 [18].
[18]. [19],
[19],