 Теорема на Ричи
Теорема на Ричи
Този текст подпомага разбирането на математическия апарат в
Общата Теория на Относителността (ОТО).
Трябва да сте гледали Матрицата I, Матрицата II и Матрицата III.
Важни са и статиите Ковариантна производна на вектор
и Символи на Кристофел.
Ковариантни индекси за производната на вектори
Ковариантната производна беше дефинирана в едноименната статия само за
вектори. Изразена в обичайни (контравариантни) компоненти, тя е:
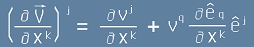 [1],
[1],
или изразена чрез Гама-символите на Кристофел от втори род:
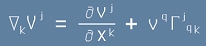 [2].
[2].
Да видим как биха изглеждали тези изрази ако представим същия вектор в ковариантни компоненти, следвайки аналогия от "Ковариантна производна". По правилото на Лайбниц, за целия вектор производната за ковариантен вектор в дуален базис е
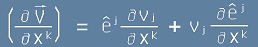 [3],
[3],
а изразена чрез ковариантни компоненти изглежда като
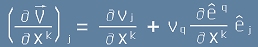 [4]. (виж как стигнахме до [4] от статията "Ковариантна производна")
[4]. (виж как стигнахме до [4] от статията "Ковариантна производна")
За да сведем второто събираемо до израз с Гама-символ, ще се наложи малко да го преобразуваме.
Да забележим, че
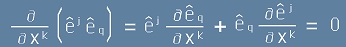 , защото в скобите отляво стои твърда единица. Следователно
, защото в скобите отляво стои твърда единица. Следователно
 . [5]
. [5]
Замeстваме [5] в [4] и получаваме:
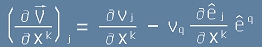 . [6], където вече е възможна замяна с Гама-символи:
. [6], където вече е възможна замяна с Гама-символи:
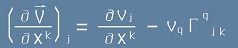 . [7]
. [7]
От [1] и [7] вече имаме представа за ко и контравариантни компоненти при производните на вектори - така вече можем да напишем как изглежда една
Ковариантна производна на тензор
Ако един тензор Т има два контравариантни индекса, неговата ковариантна производна - виж [2] - ще изглежда така:
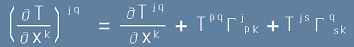 . [8]
. [8]
Ако тензорът Т е с два ковариантни индекса, то - виж [7] - ще получим:
 . [9]
. [9]
И за смесен тип (1,1) :
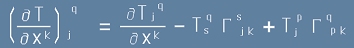 . [98]
. [98]
Сега вече е лесно да обявим споменатата в заглавието теорема на Ричи, която гласи:
Ковариантната производна на метричния тензор е нула
Доказателство:
Да заменим буквата T от [9] с друга буква g - която според традицията означава метричен тензор:
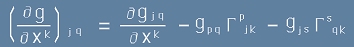 . [10]
. [10]
В статията
"Символи на Кристофел", равенство [12] беше показано, че макар Г-символите да не са тензори, първият им индекс подлежи на "вдигане" и "сваляне" чрез метричния тензор. Следователно горното равенство [10] е еквивалентно на
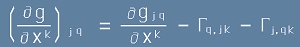 . [11]
. [11]
Да заместим последните две съставки вдясно на [11] с изразените в равенство [11] от статията "Символи на Кристофел" Гама-символи от първи род:
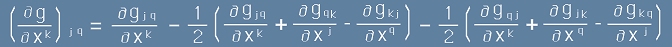 . [12]
. [12]
Ако проследим всяко събираемо от [12], имайки предвид симетрията на метричния тензор
( gjq = gqj ),
е видимо, че то действително е равно на нула.
коментари
Радостин Желязков 30.11.2010
________________________________________________________________________________________
учебни статии по физика
 Теорема на Ричи
Теорема на Ричи
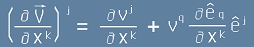 [1],
[1],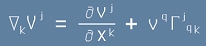 [2].
[2].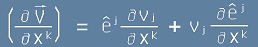 [3],
[3],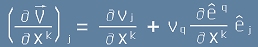 [4]. (виж как стигнахме до [4] от статията "Ковариантна производна")
[4]. (виж как стигнахме до [4] от статията "Ковариантна производна")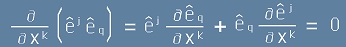 , защото в скобите отляво стои твърда единица. Следователно
, защото в скобите отляво стои твърда единица. Следователно . [5]
. [5]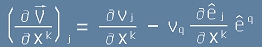 . [6], където вече е възможна замяна с Гама-символи:
. [6], където вече е възможна замяна с Гама-символи: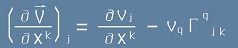 . [7]
. [7]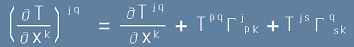 . [8]
. [8] . [9]
. [9]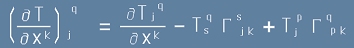 . [98]
. [98]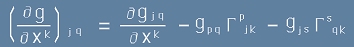 . [10]
. [10]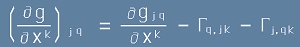 . [11]
. [11]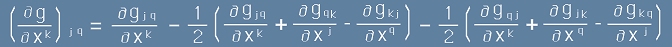 . [12]
. [12]